히프(heap)란?

히프는 우선순위 큐를 구현하는 데 자주 사용된다. 우선순위 큐에서는 우선순위가 가장 높은(또는 낮은) 원소를 먼저 삭제한다. 히프에 대한 설명을 하기 전에 최대 트리와 최소 트리에 대한 설명을 먼저 진행한다.

최대 트리 란 각 노드의 키 값이 그 자식의 키 값보다 작지 않은 트리이며, 최소 트리 란 각 노드의 키 값이 그 자식의 키 값보다 크지 않은 트리를 말한다.

여기서 최대 히프 란 최대 트리이면서 완전 이진트리이며, 최소 히프 란 최소 트리이면서 완전 이진트리를 의미한다.

이러한 최대 히프 및 최소 히프에서는 부모를 쉽게 찾아 삽입이 가능하다.

히프의 생성은 C를 통하여 다음과 같이 구현한다.

#define MAX_ELEMENTS 200
#define HEAP_FULL(n) (n==MAX_ELEMENTS-1)
#define HEAP_EMPTY(n) (!n)
typedef struct{
  int key;
  } element;

element heap[MAX_ELEMENTS];
int n=0;

최대 히프에서의 삽입

최대 히프에서 원소를 삽입하는 경우 추가되는 원소가 가장 아래부터 루트 쪽으로 올라가는 bubbling up 기법이 사용된다. 다음은 최대 히프에서의 원소의 삽입을 구현한 C 프로그램이다.

#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENTS 200 /*최대 히프 크기 +1*/
#define HEAP_FULL(n) (n == MAX_ELEMENTS-1)
#define HEAP_EMPTY(n) (!n)

typedef struct element{
  int key;
}element;

element heap[MAX_ELEMENTS];
int n=0;

void push(element item, int *n)
{
  int i;
  if(HEAP_FULL(*n)){
    fprintf(stderr, "The heap is full. \n");
    exit(EXIT_FAILURE);
  }
  i = ++(*n);
  while ((i != 1) && (item.key > heap[i/2].key)){
    heap[i] = heap[i/2];
    i /= 2;
  }
  heap[i] = item;
}
int main()
{
    struct element node1 = {7};
    struct element node2 = {16};
    struct element node3 = {49};
    struct element node4 = {82};
    struct element node5 = {5};
    struct element node6 = {31};
    struct element node7 = {6};
    struct element node8 = {2};
    struct element node9 = {44};
    push(node1, &n);
    push(node2, &n);
    push(node3, &n);
    push(node4, &n);
    push(node5, &n);
    push(node6, &n);
    push(node7, &n);
    push(node8, &n);
    push(node9, &n);
    for(int k=1;k<10;k++){
        printf("%d ",heap[k].key);
    }
    return 0;
}

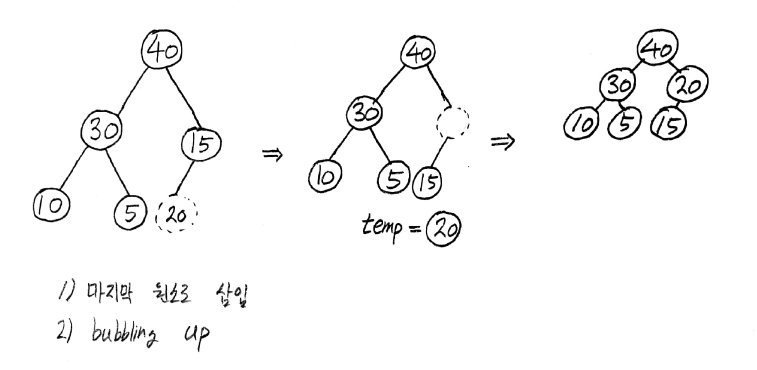
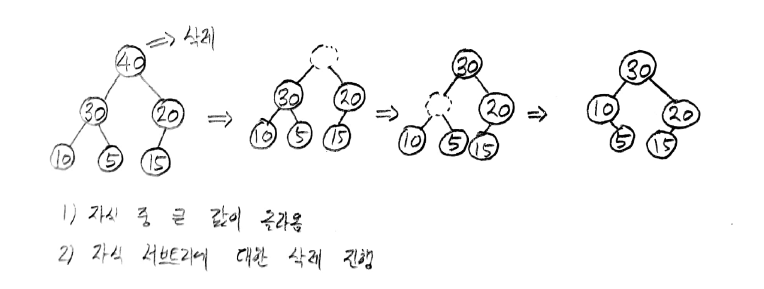
최대 히프에서의 삭제

최대 히프에서 원소의 삭제는 제일 위에서 이루어 진다. 먼저, 키값이 가장 큰 원소를 삭제하고 마지막 원소를 제거하고 두 자식 노드중 큰 값이 위로 올라가고 아래를 메꾸는 방식으로 진행된다. 최대 히프의 삭제를 구현한 프로그램은 다음과 같다.

element pop(int *n)
{
  int parent, child;
  element item, temp;
  if(HEAP_EMPTY(*n)){
    fprintf(stderr, "The heap is empty\n");
    exit(EXIT_FAILURE);
  }

  item=heap[1];
  temp = heap[(*n)--];
  parent = 1;
  child = 2;
  while(child <= *n){
    if((child < *n) && (heap[child].key < heap[child+1].key))
      child++;
    if(temp.key > heap[child].key) break;
    heap[parent] = heap[child];
    parent = child;
    child *= 2;
  }
  heap[parent] = temp;
  return item;
}

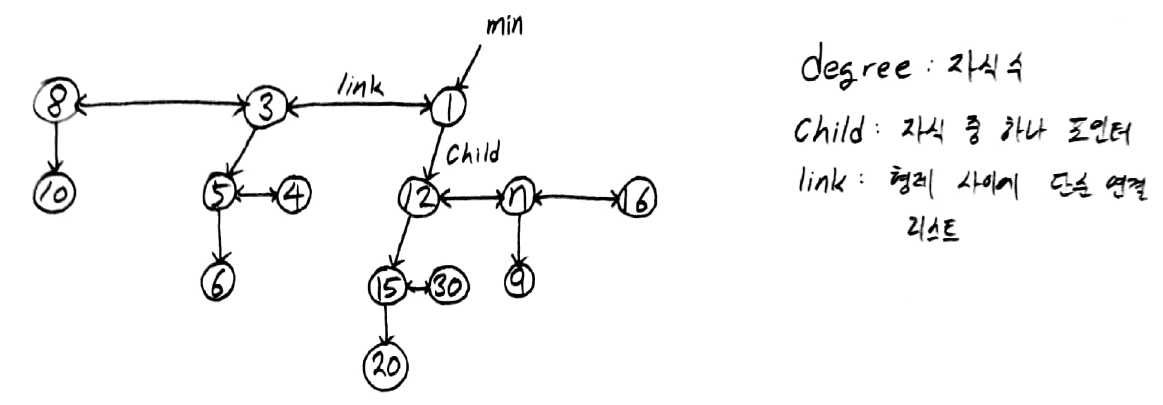
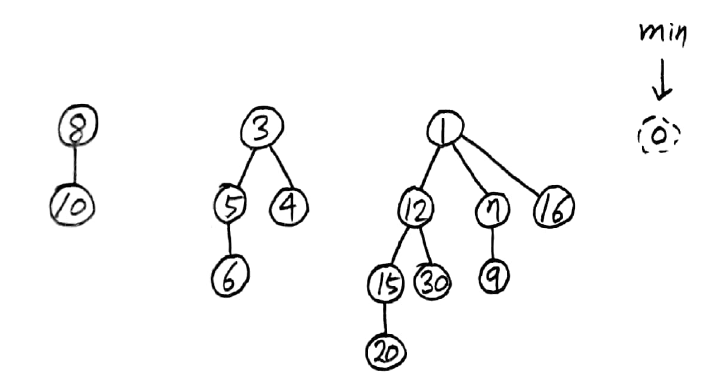
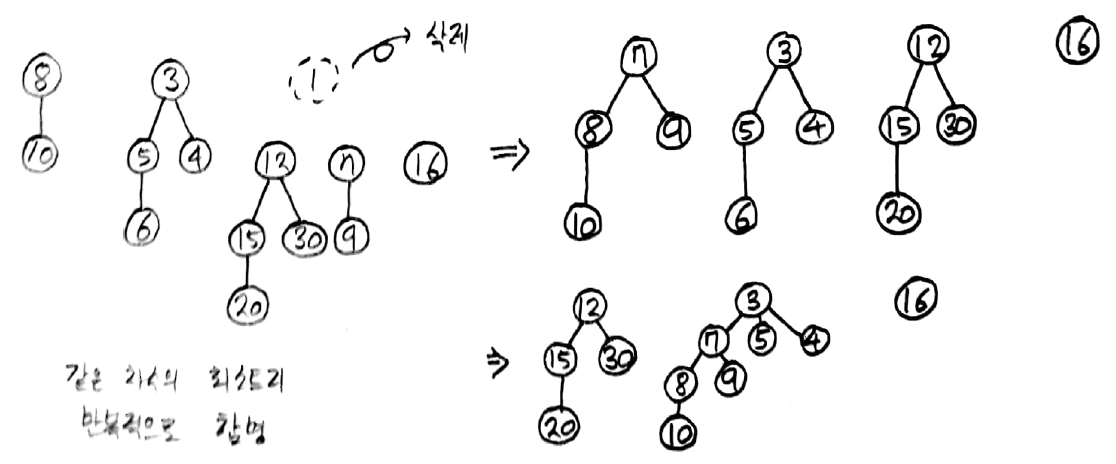
B - 히프

B - 히프란 최소 트리의 집합이다.